Statistical Consultants Ltd |
      |
Utility Functions
Economics Utility is a term used by economists, to describe the level of satisfaction an individual gets, especially from the consumption of goods and services. For most, if not all individuals, utility would increase at a decreasing rate with respect to consumption (in terms of $ spent). If the utility function is graphed, it would look something like this:  If the consumption is treated as the quantity of goods/services consumed (instead of $ amount), the utility function would depend on how the goods/services relate to each other. For example, let’s say that total utility is determined by the consumption of two goods. If the two goods are perfect substitutes, total utility would depend on a linear combination of the quantities of each good consumed. If the two goods are perfect complements, the total utility would equal the utility gained from the good consumed in the smallest quantity. If the two goods are neither perfect substitutes nor perfect complements, and both goods yield utility for the individual, the utility function would lie somewhere between the perfect substitutes and perfect complements utility functions. Total utility would be a function that increases at a decreasing rate with respect to the quantities of each good consumed. These functions can be graphed, using indifference curves. Each point on an indifference curve represents an equal amount of utility. The further the curve is from the origin, the higher the level of utility. 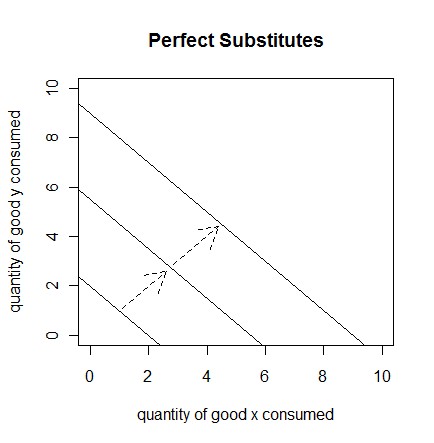 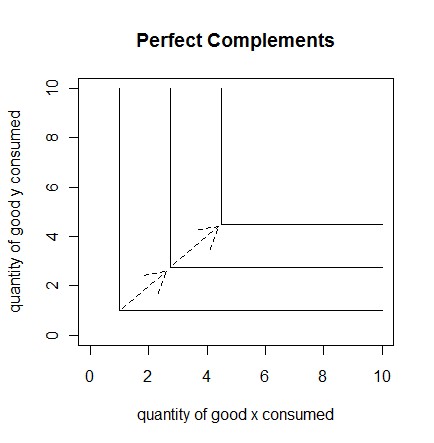 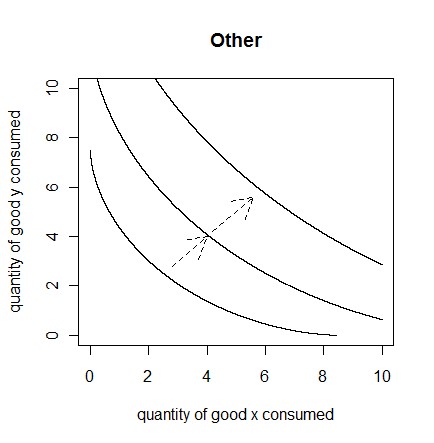 See also: |
      |
| Copyright © Statistical Consultants Ltd 2010 |