Statistical Consultants Ltd

Social Welfare Functions

Economics, Mathematics

Utility is a term used by economists to describe the level of an individual's satisfaction, especially from the consumption of goods and services.

There are various theoretical measures of a society’s collective utility i.e. its social welfare. Various social welfare functions (SWF) have been suggested, that are functions of a society’s individual level utilities.

Utilitarian

One of the utilitarian measures of a society’s welfare is the sum of all individual utilities:

utilitarian welfare formula (total)

Where:

W is the society’s welfare (collective utility)
U_i is the utility of individual i
N is the total number of people in society

Alternatively, the utilitarian measure could instead take the average (mean) utility rather than the total.

utilitarian welfare formula (average)

Rawlsian

The Rawlsian measure of society’s welfare equals the utility of the individual who is worst off.

Rawlsian welfare formula

Bernoulli-Nash

The Bernoulli-Nash SWF goes some way to find a mix of the utilitarian and Rawlsian SWFs.

They are similar to the utilitarian SWFs, b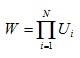ut are multiplicative rather than additive.

Bernoulli-Nash SWF (total):

Bernoulli-Nash SWF total

Bernoulli-Nash SWF (average):

Bernoulli-Nash SWF average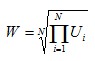

Note that this average is the geometric mean utility.

Iso-elastic

It is possible to take a more generalised mix of the utilitarian and Rawlsian welfare functions. One way is to use an iso-elastic welfare function:

Iso-elastic welfare formula

Where a is a constant and is greater than or equal to zero.

If a = 0, the SWF is utilitarian (total)
As a approaches 1, the SWF becomes Bernoulli-Nash (total)
As a approaches ∞, the SWF becomes Rawlsian

Graphing SWFs with indifference curves

The social welfare functions described above can be graphed using indifference curves. Each point on an indifference curve represents an equal amount of welfare. The further the curve is from the origin, the higher the level of welfare.

For a two person society, the indifference curves for the SWFs would look like the following: