Statistical Consultants Ltd |
      |
Axiomatic Analysis of Elementary IndicesEconomics, Economic / Financial Data Before reading this feature, it may help if you first read: Elementary Indices. Elementary index calculation methods can be tested against various axioms, to investigate whether or not they have certain desirable properties. Some axioms are more important than others. AxiomsFor each of the following axioms: n
is
the sample size of the good being surveyed
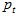 are the prices of the good at the current period
are the prices of the good at the current period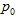 are the prices of the good at the base period
are the prices of the good at the base periodP is the elementary price index and is a function of the current and base period prices Continuity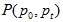 is a
continuous function of n positive
base period prices and
n
positive current period prices.
is a
continuous function of n positive
base period prices and
n
positive current period prices.IdentityThe index at the base period equals one.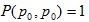 Monotonicity in Current Period Prices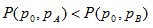 if
if 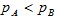 Monotonicity in Base Period Prices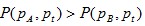 if
if 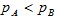 Proportionality in Current Period Prices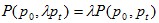 if
if 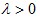 Inverse Proportionality in Base Period Prices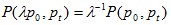 if
if 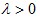 Mean Value TestThe price index lies between the smallest and biggest price ratios.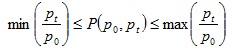 Symmetric Treatment of Establishment / ProductsIf there is a change in the ordering of establishments (or products within an establishment) the price quotations are obtained from for the two periods, the elementary index remains unchanged.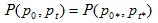 where
where 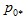 and
and 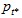 denote
the same permutation of the components of
denote
the same permutation of the components of 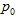 and
and 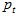 . .Price-Bouncing TestA more generalised (and more controversial) version of the previous axiom, the price-bouncing test allows for different permutations between the base and current periods.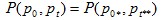 where
where 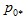 and
and 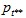 denote
possibly different permutations of the
components of
denote
possibly different permutations of the
components of
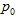 and and
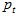 . .Time Reversal Circularity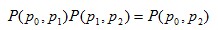 CommensurabilityThe units of measurement for each product have no effect on the price index.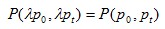 How the elementary indices compare
Jevons index satisfies all of the axioms described here. In some countries (including A problem with the Dutot index (and ratio of harmonic means) is that it doesn’t satisfy the commensurability axiom. This means that if the units of measurement change for a product, it would affect the price index. For some products, this won’t be a problem. The Carli index and the harmonic mean of price relatives don’t satisfy the price bouncing test, time reversal or circularity. The inability for time reversal is the biggest of these problems, but can be solved by taking the geometric mean of the two indices i.e. by using a Carruthers / Sellwood / Ward / Dalén index. The inability for time reversal has meant the Carli index is upwardly biased, and the harmonic mean of price relatives is downwardly biased. See also:Elementary IndicesDifferent ways of measuring the Consumer Price Index ( Index Numbers |
      |
| Copyright © Statistical Consultants Ltd 2011 |